Eigenmode expansion
Eigenmode Expansion (EME) is a computational electrodynamics modelling technique. It is also referred to as the mode matching technique or the Bidirectional Eigenmode Propagation method (BEP). Eigenmode expansion is a linear frequency-domain method.
Contents |
Principles of the EME method
Eigenmode expansion is a rigorous technique to simulate light propagation which relies on the decomposition of the electromagnetic fields into a basis set of local eigenmodes at each z-position. The eigenmodes are found by solving Maxwell's equations in each local cross-section.
In a typical waveguide, there are a few guided modes (which propagate without coupling along the waveguide) and an infinite number of radiation modes (which carry optical power away from the waveguide). The guided and radiation modes together form a complete basis set. Many problems can be resolved by considering only a modest number of modes, making EME a very powerful method.
As can be seen from the mathematical formulation, the algorithm is inherently bi-directional. It uses the scattering matrix (S-matrix) technique to join different sections of the waveguide or to model nonuniform structures.
Mathematical formulation
In a structure where the optical refractive index does not vary in the z direction, the solutions of Maxwell's equations take the form:
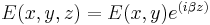
We assume here a single wavelength and time dependence of the form 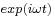 .
.
Mathematically 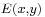 and
and 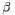 are the eigenfunction and eigenvalue of the solution which has a simple harmonic z-dependence.
are the eigenfunction and eigenvalue of the solution which has a simple harmonic z-dependence.
We can express any solution of Maxwell's equations in terms of a superposition of the forward and backward propagating modes:
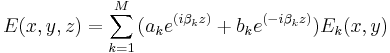
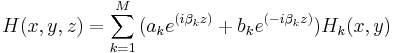
These equations provide a rigorous solution of Maxwell's equations in a linear medium, the only limitation being the finite number of modes.
Strengths of the EME method
The EME method is ideal for the modelling of guided optical components, for fibre and integrated geometries.
The method is fully vectorial (provided that it relies on a fully vectorial mode solver) and fully bidirectional.
As it relies on a scattering matrix approach, all reflections taken into account.
Unlike the beam propagation method, which is only valid under the slowly varying envelope approximation, eigenmode expansion provides a rigorous solution to Maxwell's equations.
It is generally much more efficient than FDTD as it does not require discretisation along the direction of propagation.
The scattering matrix approach provides a flexible calculation framework, potentially allowing users to only re-calculate modified parts of the structure when performing parameter scan studies.
Limitations of the EME method
EME is limited to linear problems and may be inefficient to model structures requiring a very large number of modes.